1. 결합확률
1) 결합확률 : 사건 X, Y가 동시에 발생할 확률
2) 이산형 결합 확률분포 : 두 확률변수 X 와 Y가 동시에 각각 x,y 값을 가질 확률
$f(x,y)=P(X=x,Y=y)$
$0\leq f(x,y)\leq 1$
$\sum_{x} \sum_{y} f(x)=1$
2) 연속형 결합 확률분포 :
$P(a<X<b , c<Y<d)=\int_{a}^{b}\int_{c}^{d}f(x,y)dydx$
$\int_{-\infty }^{\infty }\int_{-\infty }^{\infty }f(x,y)dydx=1$
$0\leq f(x,y)$
3) 예제1 : 주사위를 두번 던지는 행위에서 눈의 최대치 X 와 눈의 최소치 Y의 결합확률분포
X: 1,2,3,4,5,6
Y: 1,2,3,4,5,6
확률변수 $X,Y$가 $x \leq y$ 값을 만족하는 확률

①$P_{XY}(1,1)$ 는 $x=y$를 만족하며 $= \frac{1}{6}\times \frac{1}{6}=\frac{1}{36}$
②$P_{XY}(2,1)$ 는 $x>y$를 만족하며 $(2,1), (1,2)$ 의 경우의 수가 있으므로
$= 2\times \frac{1}{6}\times \frac{1}{6}=\frac{2}{36}$
③$P_{XY}(0,1)$ 는 $x>y , x=y$를 만족하지 못하므로 0
2. 주변확률
1) 주변확률 : 결합되지 않는 개별 사건의 확률 P(A) 또는 P(B)
2) 이산형
$f_X(x)= \sum_{y} f(x,y)$
$f_Y(y) = \sum_{x} f(x,y)$
2) 연속형
$f_X(x)= \sum \int_{-\infty }^{\infty }f(x,y)dy$
$f_Y(y)= \sum \int_{-\infty }^{\infty }f(x,y)dx$
2) 예제 1 이어서 주변확률분포 구하기
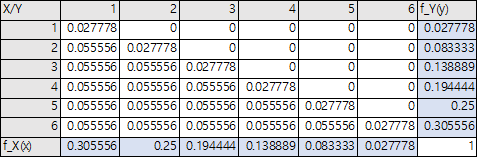
&$f_X(x) = \sum_{y=1}^{x-1}\frac{2}{36}+\frac{1}{36}=\frac{1+2(x-1)}{36}, x=1,....,6$
$f_Y(y) = \sum_{x=y+1}^{6}\frac{2}{36}+\frac{1}{36}=\frac{1+2(6-y)}{36}, y=1,....,6$
3) 예제 2 : 결합확률분포함수 $f(x,y)= c(x+y), x=0,1,2,3,4; y=0,1,2,3$
확률분포함수가 되도록 상수 c와 주변확률분포, 기댓값을 구하라
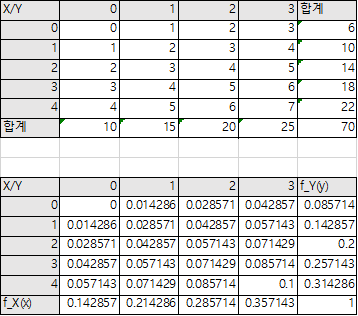
① $\sum_x\sum_yf(x,y) = c\sum_x^4\sum_y^3f(x+y) = 70c= 1 \rightarrow c=\frac{1}{70}$
② $f_X(x) = \frac{1}{70}\sum_{y=0}^3(x+y)=\frac{4x+6}{70} , x=0,1,2,3,4$
$f_X(x) = \frac{1}{70}\sum_{x=0}^4(x+y)=\frac{5x+10}{70} , y=0,1,2,3$
3. 조건부확률
1) 조건부확률 : 사건 B가 사실일 경우 사건 A에 대한 확률
$P(A|B)=\frac{P(A,B)}{P(B)}$
2) 예제1 이어서 Y=y일 때, X의 조건부확률분포
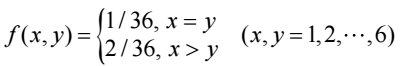

$f(x|y)= \frac{f(x,y)}{f_Y(y)}= \frac{\frac{1}{36}}{\frac{1+2(6-y)}{36}} = \frac{1}{1+2(6-y)} , x=y$
$f(x|y)= \frac{f(x,y)}{f_Y(y)}= \frac{\frac{2}{36}}{\frac{1+2(6-y)}{36}} = \frac{2}{1+2(6-y)} , x>y$
4. 독립
1) 독립 : 두 사건 A, B가 $P(A,B) = P(A)P(B)$ 의 관계가 성립하면 둘은 서로 독립이라고 정의한다
2) 예제 1 이어서 X,Y의 독립성 검토

$f(1,1) = \frac{1}{36} , f_X(1) = \frac{1}{36} , f_Y(1) = \frac{11}{36}$
2) 예제 1 이어서 X,Y의 독립성 검토

$f(1,1) = \frac{1}{36} , f_X(1) = \frac{1}{36} , f_Y(1) = \frac{11}{36}$ → 독립x
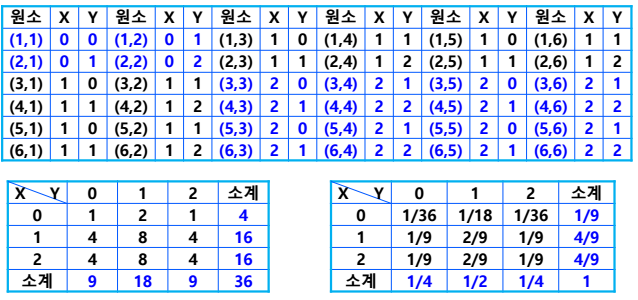
2) 예제 2 주사위를 두번 던지는 시행에서 3이상 눈의 개수 X와 짝수 눈의 개수 Y의 독립성 검토
'School Activities > Math' 카테고리의 다른 글
| [확률과 통계] 정규분포와 표준정규분포 (0) | 2019.10.13 |
|---|---|
| [확률과 통계] 확률변수와 확률분포 , 척도 (0) | 2019.10.12 |
| [확률과 통계] 대푯값과 산포도 (0) | 2019.10.12 |
| [확률과 통계] 그래프 그리기 (0) | 2019.10.12 |